Solving Project Euler Problems 161 (Trominoes Tiling) and 185 (Number Mind) with ZDDs
In this post, I describe how ZDDs (Zero Decision Diagrams) helped me crack two challenging Project Euler (PE) problems. See my earlier post on ZDDs to learn more.
My experience with Project Euler Problems
As I attempted to solve more and more problems, I found a disproportionately large number of them centered around the theory of numbers. These involved important ideas of number sieves, congruences, continued fractions, the Farey series, solving Pell’s equation, implementing Shanks Tonelli algorithm etc., and had me sifting through Hardy and Wright’s book every so often.
But after a while they weren’t so much fun. I did, however, find enough problems of my interest to get me hooked — enumeration and dynamic programming (208, 161, 209, 172, 169, 215, 219), probability (227, 213) and those occasionally unique ones like 197 (concerning the “steady-state” behavior of a certain sequence). Working through these problems made me realize what a treasure PE was. Kudos to Colin “Euler” Hughes and the PE-team for their effort in running this great site!
In addition to having the fun of solving the problems myself, I could study the solutions worked out by other members in the forum. Seeing the elegance, efficiency and analyses of some of their solutions was a rewarding (even if a bit humbling) experience. A case in point is the solution to Robot Walks (208) by sajninredoc and stijn263 (among others), where they reduce the enumeration problem to a single summation. And then there were those APL/J programmers with their cute one-liners!
In this entry, I shall outline my solutions (and their performance characteristics) to the Trominoes Tiling (161) and Number Mind (185) problems. To solve these problems, I used the ZDD techniques I had just studied in Knuth’s pre-fascicle (now in print as TAOCP Volume 4A: Combinatorial Algorithms, Part 1). I had blogged earlier Knuth’s Fun with ZDDs musing.
Trominoes Tiling (161): Enumerating Exact Covers using ZDDs
Trominoes Tiling (161) is almost the tiling problem of TAOCP 7.1.4 — (130) with the difference that only trominoes are allowed (no monominoes or dominoes) and the grid-size is slightly larger (9x12 instead of 8x8). I reuseed, with the obvious changes, the ZDD routines that I had coded while working out that section. Since Knuth has already explained the ideas involved so beautifully (see the text around 7.1.4 — (129)), I shall only briefly sketch the ZDD construction before giving some performance statistics.
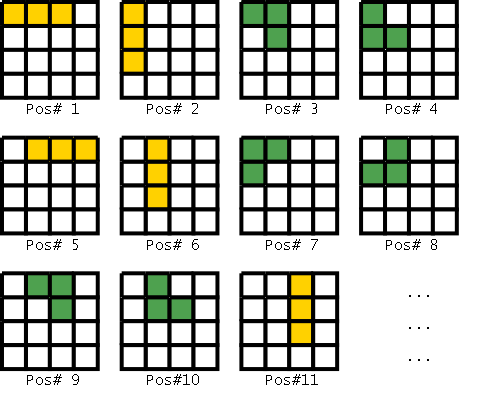
To begin, we first model the tiling problem as an Exact Cover. This involves creating a boolean matrix \((a_{ij})\) of 9x12 = 108 columns (corresponding to cells of the board) and 526 rows (corresponding to the ways of placing the L and I trominoes in all possible orientations on a 9x12 grid). We have \(a_{ij} = 1\) iff tromino placement \(i\) occupies cell \(j\). The strategy for placement numbering I used is shown below for the simpler 4x4 case (the cells are numbered in the usual row-major order). Since the placement strategy decides the variable-ordering of the ZDD and hence its size (unless, of course, we choose to sift/reorder variables later on), it is important to pick a placement strategy that is not too inefficient.

Having constructed the boolean matrix, to enumerate the tilings, we find the number of ways to select some rows of the matrix such that if we inspect any column, precisely one of the selected rows contains a 1 in that column. Hence the name “exact” cover — we neither want to leave any cell uncovered, nor do we want parts of two or more trominoes to overlap.
Exact covers can be enumerated using Knuth’s Algorithm X — an efficient backtracking technique implemented using an idea Knuth calls Dancing Links (DANCE program, paper at arXiv, Computer Musing video). Algorithm X not only enumerates the solution, it in fact generates them all!
To enumerate exact covers using ZDDs, using the \(m\times n\) matrix \((a_{ij})\) produced in the step above, we construct the boolean function (Eq. 7.1.4 — (129)):
\[f(x_1,\ldots,x_m) = \bigwedge_{j=1}^n S_1(X_j)\]where boolean variable \(x_i\) indicates selection of row \(I\) of the matrix (that is, placement a tromino in the orientation \(I\)), \(X_j\) = \(\{x_i \bar a_{ij} = 1\}\) is the set of rows \(i\) that have a 1 in column \(j\), and \(S_1\) is the Symmetric Boolean Function that is true if exactly one of its inputs are true. The function \(f\) will be true iff for each column \(j\), exactly one of the selected row \(i\) has \(a_{ij}\) = 1 – this is just the condition for exact cover!
For various ways to efficiently construct the above ZDD, see Exercise 7.1.4 — 212. The function \(S_1\) can itself be implemented using Exercise 207’s “Symmetrizing” operation.
Once we have the ZDD for the boolean function \(f\) above, the number of solutions, i.e., the number of vectors \((x_1,\ldots,x_m)\) that make \(f\) true (which are precisely the vectors representing exact covers) can be readily found using the ZDD-analog of Algorithm 7.1.4C.
Runtime performance of the solution: The resulting ZDD involved 526 variables and had a size of 7893743 zeads. Without invoking any garbage collection, the peak memory usage was ~600MB (where each zead in my implementation was a 20-byte node); time taken was 34s (user) and 85s (elapsed). Given that my memos weren’t very optimized (I had used GCC’s std::map) and neither had I tried doing any variable reordering, the performance seemed reasonable.
A dynamic programming approach (like one I later used for Crack-free Walls (215)), should have been able to give the results in about a second (this was confirmed by posts on the forum). Nevertheless, the ZDD solution was fast enough to keep my conscience clear of any violations of Project Euler’s one-minute-rule.
Aside: The Crack-free Walls (215) problem is kind of like TAOCP Exercise 7.1.4 — 214 (Knuth calls it “faultfree”) and should be amenable to the ZDD attack. There, however, appears to be a danger of hitting space-out since the grid-size 10x32 is somewhat large. I’ve not tried this approach.
Number Mind (185): Using ZDDs to satisfy an ad-hoc set of constraints
Number Mind (185) was the other PE problem that I solved with ZDDs. In this problem we’re to uncover a 16-digit number given a set of “guesses” of the form:
5616185650518293 ;2 correct
3847439647293047 ;1 correct
5855462940810587 ;3 correct
...
The guesses along with the “hit-rates” provide partial information about the secret number. Our aim is to find the “secret” number corresponding to the set of guesses. To solve this problem, we create variables \(x_{i,j}\) representing the condition that \(i\)th digit (\(1\leq i\leq 16\)) is \(j\) (\(0\leq j\leq 9\)). We then have the following constraints:
- Since each position \(i\) can hold just one digit, for each \(i\) exactly one of \(x_{i,j}\) can be true. Constraints of this kind correspond to terms like \(S_1(x_{i0},\ldots,x_{i9})\), where \(S_1\) is again our friend, the symmetric boolean function.
- Each of the given guess “hit-rates” must be satisfied. As an example, the third constraint
5855462940810587 (3 correct)is represented as:
Using the symmetrizing operator from Exercise 7.1.4 — 207, both the above kinds of constraints are easily represented. Finally, we compute the AND (or, INTERSECT, if one prefers family-of-subsets point-of-view) of the individual constraints — and we’re left with the final ZDD representing the family of feasible solutions (in our case, the solution in fact turns out to be unique).
Runtime performance of the solution: The ZDD had 160 variables \(x_{i,j}\), program execution had a peak memory usage of ~1GB without any garbage collection or reordering (zead-size 20-bytes), size of the largest partial function was 4665450 zeads. The running time was ~16s (both user and elapsed).
Conclusion
Comparing the ZDD solutions to the two PE problems, I think it was the kind of “unstructured” problem like Number Mind where the ZDD technique really shined.